PgRouting

A pgRouting egy nyílt forráskódú, C++ nyelven írt bővítmény a PostGIS/PostgreSQL térinformatikai adatbázisokhoz. Lehetővé teszi gráf adatszerkezetek kezelését, így például legrövidebb utakat, csomópontok távolságát és egyéb hálózati elemzést igénylő feladatokat oldhatunk meg vele. A programcsomag GNU GPL v2 licenc alatt használható.

Telepítés

A PostGIS újabb verziói (2.0+) már tartalmazzák a pgRouting csomagot, így nem szükséges külön telepíteni, csak aktiválni kell, a következő módon.

CREATE EXTENSION pgrouting;

A teljes telepítési útmutató elérhető a pgRouting honlapján.

Felépítés

A pgRouting két fő összetevőből áll:

• Egy C modul, amely egy PostgreSQL-ben átadott lekérdezést használ a gráf felépítéséhez.
• C++ modulok, amelyek a lekérdezést úgynevezett boost gráffá alakítják, és futtatják az útvonal-választást.

Hogy mely összetevőt használja a program futása során, az az algoritmus fajtájától függ.

A függvénykönyvtár szerkezete pedig a következőképp néz ki:

  cmake/                 - cmake fájlok
  CMakeLists.txt         - Top level cmake 
  doc/                   - Top level doc, a nem forrásalgoritmus-specifikus dokumentáció helye
    themes/              - Sphinx téma a doc-nak
    static/              - dokumentáció képei
  src/                  
    astar/               - A* algoritmus
    common/              - pgRouting projektekben szükséges közös fájlok
    dijkstra/            - Dijkstra algoritmus
    driving_distance/    - Vezetési távolság
    trsp/                - Legrövidebb utak kanyarodási korlátokkal
    tsp/                 - Utazó ügynök
  tools/                 - Tesztelési eszközök

Az src mappa minden könyvtárában doc, sql, src, és test almappák találhatók, melyekbe értelemszerűen a következők kerülnek:

• doc: Az adott algoritmushoz szükséges összes dokumentáció ReStructuredText formátumban. Ennek célja, hogy a függvények leírásával, input és output paraméterek megadásával a felhasználók számára érthetővé tegye, hogyan működik az algoritmus.
• sql: Az sql burkolók a C kódhoz.
• src: C/C++ kód az algoritmushoz.
• test: test.conf, *.data, *.test, és *.rest fájlok az algoritmus teszteléséhez.

Fejlesztési célból a programot klónozhatjuk Git-en keresztül, majd telepítjük a következők szerint:

 git clone git@github.com:pgRouting/pgrouting.git
 cd pgrouting
 cmake -DWITH_TSP=ON -DWITH_DD=ON .
 make
 sudo make install

Használat

Adatok betöltése

A vektoros térképi adatok adatbázis-táblába betöltésére számos eszköz áll rendelkezésre, például:

• osm2po: OpenStreetMap (OSM) adatok konvertálása SQL formátumba, pgRouting-nak megfelelő formátumban.
• shp2pgsql: PostgreSQL shapefile betöltője.
• ogr2ogr: Vektoros adatok konverziója.
• osm2pgsql: OSM adat betöltése postgreSQL-be.

Előfeldolgozás

Amikor egy GIS fájlt olvasunk be az adatbázisunkba a pgRouting számára, nem feltétlenül követnek alkalmas topológiát a rekordok. A helytelen topológia hibás útvonalakhoz vezetne. Hogy használható adattáblát kapjunk, csomópontokra van szükségünk minden egyes útkereszteződésnél. Az útvonalhálózat megfelelő topológiájának kialakítását segítheti a pgr_createTopology vagy a pgr_nodeNetwork parancs. Működésük hasonló. Az utóbbi beolvassa a „csúcstalan” hálózat adatbázis-tábláját, majd egy új táblába írja a már felcsúcsozott éleket. Paraméterei

• éltábla neve,
• tolerancia: a toleranciaértéken belüli csomópontok egy csomópontot fognak alkotni,
• id, az éltábla elsődleges kulcsa,
• geometriát tartalmazó oszlop,
• kimeneti tábla szuffixe. Alapértelmezetten edge_table_noded.

Lekérdezés szintaxis

Minden pgRouting lekérdezés az alábbi formátumot követi:

SELECT pgr_<algorithm>(<SQL for edges>, start, end, <additonal options>)

ahol a pgr_előtaggal hívjuk meg a lentebb ismertetett algoritmusok egyikét. A belső SQL lekérdezéssel adjuk meg a táblát, amelyre az algoritmust futtatjuk, a kezdő- és végponto(ka)t, valamint opcionális további szűrési feltételeket. Például, ha a pgRouting dokumentációjában bemutatott mintaadatokkal dolgozunk, az alábbi lekérdezéssel a 2. sorszámú csúcsból a 3. sorszámúba vezető legrövidebb utat kapjuk meg:

 SELECT * FROM pgr_dijkstra(
      'SELECT id, source, target, cost, reverse_cost 
      FROM edge_table', 2, 3);

Algoritmusok

Dijkstra algoritmus

A Dijkstra algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából egy másik adott csúcsába vezető legrövidebb út megtalálására szolgáló módszer. Az algoritmus csak nem negatív élsúlyok esetén működik. Jelölje a súlyfüggvényt $w$. Az algoritmus mohó módszert használ. Legyen a kiindulási pont $s$, a célállomás pedig $t$. Az algoritmus egy $H$ halmazban tárolja azon csúcsokat, amelyeknek már ismerjük az $s$-ből hozzájuk vezető legrövidebb út hosszát. Ezen kívül minden $u$ csúcsról nyilvántartunk az algoritmus futása során egy $D[u]$ értéket, ami az $s$-ből $u$-ba vezető addig megismert legrövidebb út hossza.

Kezdetben $H$ üres, $D[s]=0$ és minden más $v$ csúcsra $D[v]=\infty$. Ezután minden iterációban kiválasztunk a $V\setminus H$ halmazból egy olyan $x$ csúcsot, amelyre $D[x]$ minimális, áttesszük $x$-et $H$-ba, majd $x$ minden olyan $v$ szomszédjára, amely nincs $H$-ban frissítjük a $D[v]$ értéket: $D[v]=\min\{D[v],D[x]+w(x,v)\}$. Az algoritmus véget ér, amikor $t$ átkerül $H$-ba, ekkor $D[t]$ egy legrövidebb $s$-ből $t$-be vezető út hossza. Az algoritmus kis módosítással egy legrövidebb utat is megad $s$-ből $t$-be.

Az algoritmus költsége szomszédsági mátrixos gráfábrázolás esetén $O(|V|^{2})$, szomszédsági listás gráfábrázolás esetén Fibonacci kupacot használva $O(|E|+|V|\log |V|)$.

   A Dijkstra algoritmus pgRouting lekérdezéseket használva:

Az algoritmus pgr_costResult(seq, id1, id2, cost) sorok halmazával tér vissza, melyek egy utat hoznak létre (a legrövidebb utat a két csúcs között). Ebben a seq a sorok szekvenciája, az id1 a startcsúcs azonosítója, az id2 az él azonosítója (az utolsó sorban -1), a cost az áthaladás költsége id1-től id2 élen keresztül.

pgr_costResult[] pgr_dijkstra(text sql, integer source, integer target,
                           boolean directed, boolean has_rcost);
/*Ebben a source a startcsúcs azonosítója,
a target a célcsúcs azonosítója,
a directed akkor igaz, ha az él irányított,
a has_rcost akkor igaz, ha negatív élek vannak, ekkor a kapott sorokat az algoritmus visszafelé dolgozza fel.*/

Segítségül egy olyan SQL lekérdezést használunk, amelyiknek a vizsgált gráf éleivel kell visszatérnie:

SELECT id, source, target, cost [,reverse_cost] FROM edge_table
/* Ebben az id az él azonosítója,
a source: az él startcsúcsának azonosítója,
a target az él célcsúcsának azonosítója,
a cost egy pozitív szám, az élen való áthaladásnak a költsége,
a reverse_cost opcionális, akkor lesz használva, ha a directed és a has_rcost értéke is igaz.*/

Dijkstra algoritmussal kiegészítve az előző lekérdezés reverse_cost nélkül:

SELECT seq, id1 AS node, id2 AS edge, cost
        FROM pgr_dijkstra(
                'SELECT id, source, target, cost FROM edge_table',
                7, 12, false, false
        );

Reverse_cost-tal:

SELECT seq, id1 AS node, id2 AS edge, cost
        FROM pgr_dijkstra(
                'SELECT id, source, target, cost, reverse_cost FROM edge_table',
                7, 12, true, true
        );

Jól látható, hogy a két módszer csak a directed és a has_rcost értékekben különbözik.

Kétirányú Dijkstra algoritmus

A kétirányú Dijkstra algoritmus szintén egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából egy másik adott csúcsába vezető legrövidebb út megtalálására szolgáló módszer. Az algoritmus csak nem negatív élsúlyok esetén működik. Legyen a kiindulási pont $s$, a célállomást pedig $t$. A Dijkstra algoritmust futtatjuk a kiindulási pontból az eredeti gráfon, és párhuzamosan a célállomásból a transzponált gráfon (amelyet úgy kapunk az eredeti gráfból, hogy az élek irányítását megfordítjuk). Akkor állunk meg, ha egy $v$ csúcs mindkét irányból bekerül a Dijkstra algoritmusnál definiált $H$ halmazba (pontosabban a $H_{s}$ és a $H_{t}$ halmazba is). Egy alternatív lehetőség, hogy a $H_{s}$ és a $H_{t}$ halmazok közül minden egyes iterációban csak azt bővítjük, amelyiknél $D[x]$ kisebb. Az algoritmus kis módosítással egy legrövidebb utat is megad $s$-ből $t$-be.

k-Dijkstra algoritmus

A $k$-Dijkstra algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából több adott csúcsába vezető legrövidebb út megtalálására szolgáló módszer. Valójában a Dijkstra algoritmus a gráf egy adott csúcsából az összes többi csúcsba vezető legrövidebb utat megtalálja, így akárhány célállomást megadhatunk. Az algoritmus akkor fejeződik be, amikor minden egyes célállomás bekerült a Dijkstra algoritmusnál definiált $H$ halmazba. Az algoritmus kis módosítással magukat a legrövidebb utakat is megadja.

Az algoritmus költsége szomszédsági mátrixos gráfábrázolás esetén $O(|V|^{2})$, szomszédsági listás gráfábrázolás esetén Fibonacci kupacot használva $O(|E|+|V|\log |V|)$.

A* algoritmus

Az $A^{\ast }$ algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából egy másik adott csúcsába vezető legrövidebb út megtalálására szolgáló módszer. Az $A^{\ast }$ algoritmus a Dijkstra algoritmus általánosítása, és szintén csak nem negatív élsúlyok esetén működik. Jelölje a súlyfüggvényt $w$. Az algoritmus mohó módszert használ. Legyen a kiindulási pont $s$, a célállomás pedig $t$. Az algoritmus egy $H$ halmazban tárolja azon csúcsokat, amelyeknek már ismerjük az $s$-ből hozzávezető legrövidebb út hosszát, egy $M$ halmazban pedig azokat, amelyeket már elértünk $s$-ből, de az $s$-ből hozzájuk vezető legrövidebb út hosszát még nem ismerjük. Minden $u$ csúcsról nyilvántartunk az algoritmus futása során három értéket: $D[u]$ az $s$-ből $u$-ba vezető addig megismert legrövidebb út hossza, $C[u]$ egy nem negatív heurisztikus alsó becslés az $u$-ból $t$-be vezető legrövidebb út hosszára, amelyre az is teljesül, hogy az $u$-ból bármely $v$ csúcsba vezető legrövidebb út hosszára $C[u]-C[v]$ alsó korlát (például egy térkép esetén $u$ és $t$ légvonalban mért távolsága), végül $B[u]=D[u]+C[u]$.

Kezdetben $H$ üres, $M$-ben csak az $s$ csúcs van, és $B[s]=0$. Ezután minden iterációban kiválasztunk az $M$ halmazból egy olyan $x$ csúcsot, amelyre $B[x]$ minimális, áttesszük $x$-et $H$-ba, majd $x$ minden olyan $v$ szomszédjára, amely nincs $H$-ban frissítjük először a $D[v]$ értéket: $D[v]=\min\{D[v],D[x]+w(x,v)\}$, majd a $B[v]$ értéket: $B[v]=\min\{B[v],D[v]+C[v]\}$, végül áttesszük $v$-t $M$-be. Az algoritmus véget ér, amikor $t$ átkerül $M$-ből $H$-ba, ekkor $B[t]$ egy legrövidebb $s$-ből $t$-be vezető út hossza. Az algoritmus kis módosítással egy legrövidebb utat is megad $s$-ből $t$-be.

A tapasztalat azt mutatja, hogy az $A^{\ast }$ algoritmus számos esetben hatékonyabb, mint a Dijkstra algoritmust.

Kétirányú $A^{\ast }$ algoritmus

A kétirányú $A^{\ast }$ algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából egy másik adott csúcsába vezető legrövidebb út megtalálására szolgáló módszer. Az algoritmus csak nem negatív élsúlyok esetén működik. Legyen a kiindulási pont $s$, a célállomást pedig $t$. Az $A^{\ast }$ algoritmust futtatjuk a kiindulási pontból az eredeti gráfon, és párhuzamosan a célállomásból a transzponált gráfon (amelyet úgy kapunk az eredeti gráfból, hogy az élek irányítását megfordítjuk). Akkor állunk meg, ha egy $v$ csúcs mindkét irányból bekerül az $A^{\ast }$ algoritmusnál definiált $H$ halmazba (pontosabban a $H_{s}$ és a $H_{t}$ halmazba is). Az algoritmus kis módosítással egy legrövidebb utat is megad s-ből t-be.

Yen algoritmus

A Yen algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf egy adott csúcsából egy adott másik csúcsába vezető legrövidebb út mellett megtalálja a második, harmadik, …, $k$-adik legrövidebb (egyszerű) utat is. Az algoritmus csak nem negatív élsúlyok esetén működik.

Az algoritmus költsége $O(k|V|(|E|+|V|\log |V|))$.

Floyd-Warshall algoritmus

A Floyd-Warshall algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf bármely két csúcsa közötti legrövidebb út megtalálására szolgáló módszer. Az algoritmus negatív élsúlyok esetén is működik, ha a gráf nem tartalmaz negatív összhosszúságú irányított kört. Jelölje a súlyfüggvényt $w$. Az algoritmus dinamikus programozást használ. Legyen a gráf csúcshalmaza $\{v_{1},v_{2},\ldots ,v_{n}\}$. Az algoritmus minden $0\leqslant k\leqslant n$ esetén meghatározza a $v_{i}$-ből $v_{j}$-be menő legrövidebb olyan (egyszerű) út $T_{k}[v_{i},v_{j}]$ hosszát, amelyen a közbülső csúcsok a $\{v_{1},v_{2},\ldots ,v_{k}\}$ halmazból kerülnek ki: $T_{0}[v_{i},v_{j}]=w(v_{i},v_{j})$, és $T_{k}[v_{i},v_{j}]=\min\{T_{k-1}[v_{i},v_{j}],T_{k-1}[v_{i},v_{k}]+T_{k-1}[v_{k},v_{j}]\}$ ha $k>0$. Az algoritmus kis módosítással magukat a legrövidebb utakat is megadja.

Az algoritmus költsége $O(|V|^{3})$.

Johnson algoritmus

A Johnson algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf bármely két csúcsa közötti legrövidebb út megtalálására szolgáló módszer. Az algoritmus negatív élsúlyok esetén is működik, ha a gráf nem tartalmaz negatív összhosszúságú irányított kört. Jelölje a súlyfüggvényt $w$. Az algoritmus ritka gráfokon teljesít igazán jól.

Vegyünk fel egy új $s$ csúcsot, és vezessünk $s$-ből nulla súlyú éleket $G$ csúcsaiba. Jelölje az így kapott gráfot $G'$. Futtassuk le $G'$-re a Bellman-Ford algoritmust az $s$ kezdőcsúccsal. Az algoritmus által szolgáltatott távolságérték a gráf egy $v$ csúcsára legyen $D[v]$. Átsúlyozzuk a $G$ gráf éleit: legyen $w'(u,v)=w(u,v)+D[u]-D[v]$ minden $(u,v)$ élre. Most $w'$ egy nem negatív súlyfüggvény $G$-n. Futtassuk ezzel a súlyfüggvénnyel a Dijkstra algoritmust a $G$ gráf minden csúcsából. Egy legrövidebb $u$-ból $v$-be vezető út hossza ezután a kapott érték mínusz $D[u]-D[v]$. Az algoritmus kis módosítással magukat a legrövidebb utakat is megadja.

Az algoritmus költsége szomszédsági listás gráfábrázolás esetén Fibonacci kupacot használva $O(|V|(|E|+|V|\log |V|))$.

   A Johnson algoritmus pgRouting lekérdezéseket használva:

Az algoritmus pgr_costResult(seq, id1, id2, cost) sorok halmazával tér vissza minden csúcspárra a gráfban:

pgr_costResult[] pgr_aspsJohnson(sql text); -- magyarul minden egyes csúcspárra kiszámolja az összes költséget.
/*Ebben a seq a sorok szekvenciája,
az id1 a startcsúcs azonosítója,
az id2 a célcsúcs azonosítója,
a cost az id1-től id2-ig jutás költsége.*/

Segítségül egy olyan SQL lekérdezést használunk, amelyiknek a vizsgált gráf éleivel kell visszatérnie:

SELECT source, target, cost FROM edge_table;
/* Ebben a source: az él startcsúcsának azonosítója,
a target az él célcsúcsának azonosítója,
a cost egy pozitív szám, az élen való áthaladásnak a költsége.*/

Johnson algoritmussal kiegészítve az előző lekérdezés:

SELECT seq, id1 AS from, id2 AS to, cost
    FROM pgr_apspJohnson(
        'SELECT source, target, cost FROM edge_table'
    );

Utazó ügynök probléma

Az utazó ügynök probléma a következő. Adott városoknak egy listája, és adott bármely két város között a távolság. Határozzunk meg egy olyan körutat, amely minden városon pontosan egyszer halad át, és a hossza minimális. A problémára nem ismert polinomiális költségű algoritmus. A program ún. simulated annealing technikán alapuló algoritmust használ egy jó közelítő megoldás meghatározására.

Legrövidebb utak kanyarodási korlátokkal

Az algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráf adott csúcsából egy másik adott csúcsába vezető legrövidebb út meghatározásakor képes figyelembe venni, hogy két csatlakozó él egymás utáni bejárása extra költséggel bírhat. Ezeket a megszorításokat egy külön táblában adhatjuk meg. Tapasztalat szerint az algoritmus közel olyan gyors, mint az $A^{\ast }$ algoritmus.

Vezetési távolság

Az algoritmus egy súlyozott élű, irányított $G=(V,E)$ gráfban a Dijkstra algoritmus felhasználásával megadja azon csúcsokat, melyekbe egy vagy több adott csúcsból egy adott értéknél rövidebb úton el lehet jutni.

Kapcsolódó alkalmazások

Útvonal-meghatározásra alkalmas adathalmazt például OpenStreetMap (OSM) térképekből nyerhetünk ki. Ehhez egyik alkalmas segédeszköz az OSM2PO alkalmazás, amely megfelelő topológiájú SQL fájlt állít elő a megadott térképrészlethez, amely egyből alkalmas a pgRouting-gal vagy QGIS-szel való feldolgozásra.

Útvonal megjelenítése OSM2PO webszolgáltatásként

Az OSM2PO révén vizualizálhatjuk is a legrövidebb utakat. A programmal előállított SQL táblákban minden útkereszteződéshez tartozik egy rekord, melyben a következőket tároljuk:

• koordináták (x1, x2, y1, y2),
• név (osm_name),
• csomópont azonosító (id),
• lehetséges továbbhaladási irány (osm_source_id, osm_target_id),
• útszakasz hossza (km),
• megengedett sebesség (kmh),
• költség (cost),
• geometria (geom_way).

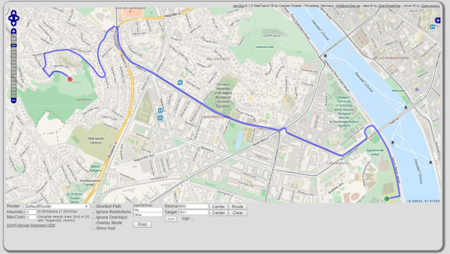
A demo.bat fájl szerkesztésével specifikálhatjuk térképünk paramétereit, például, hogy mely térképrészleten dolgozzunk. A Mapzen oldalán kész .pbf formátumú városrészleteket találhatunk, melyeket kompatibilisek az Osm2Po-val. A fájl futtatásával előáll egy .sql fájl is, melyet importálhatunk a postGIS adatbázisunkba, és akár pgRouting lekérdezéseket is futtathatunk rajta. Amíg fut a program, helyi webszerveren (localhost:8888/Osm2poService) jeleníthető meg az importált térképrészlet, melyen az útkeresést is kipróbálhatjuk.

Szakirodalom

• Regina O. Obe, Leo S. Hsu. "pgRouting: A Practical Guide", Locate Press, 2016.
• Regina O. Obe, Leo S. Hsu. "PostGIS in Action (Second Edition)", Manning Publictions (ISBN 9781617291395). 2015. pp 286-290.
• Lijing Zhang, Xuanhui He. "Route Search Base on pgRouting", Software Engineering and Knowledge Engineering: Theory and Practice Vol 2.. Springer-Verlag Berlin Heidelberg, 2012. pp 1003-1007.

Külső hivatkozások

• A pgRouting hivatalos honlapja
• pgRouting Dokumentáció
• Fejlesztőkörnyezet telepítési útmutató
• pgRouting Workshop
• OpenStreetMap fájl betöltése Osm2Po-val és útvonalkeresés